![]() Evolution of the cosmic surfaces in a closed static universe (H=Ḣ=Ḧ=0)
Evolution of the cosmic surfaces in a closed static universe (H=Ḣ=Ḧ=0)
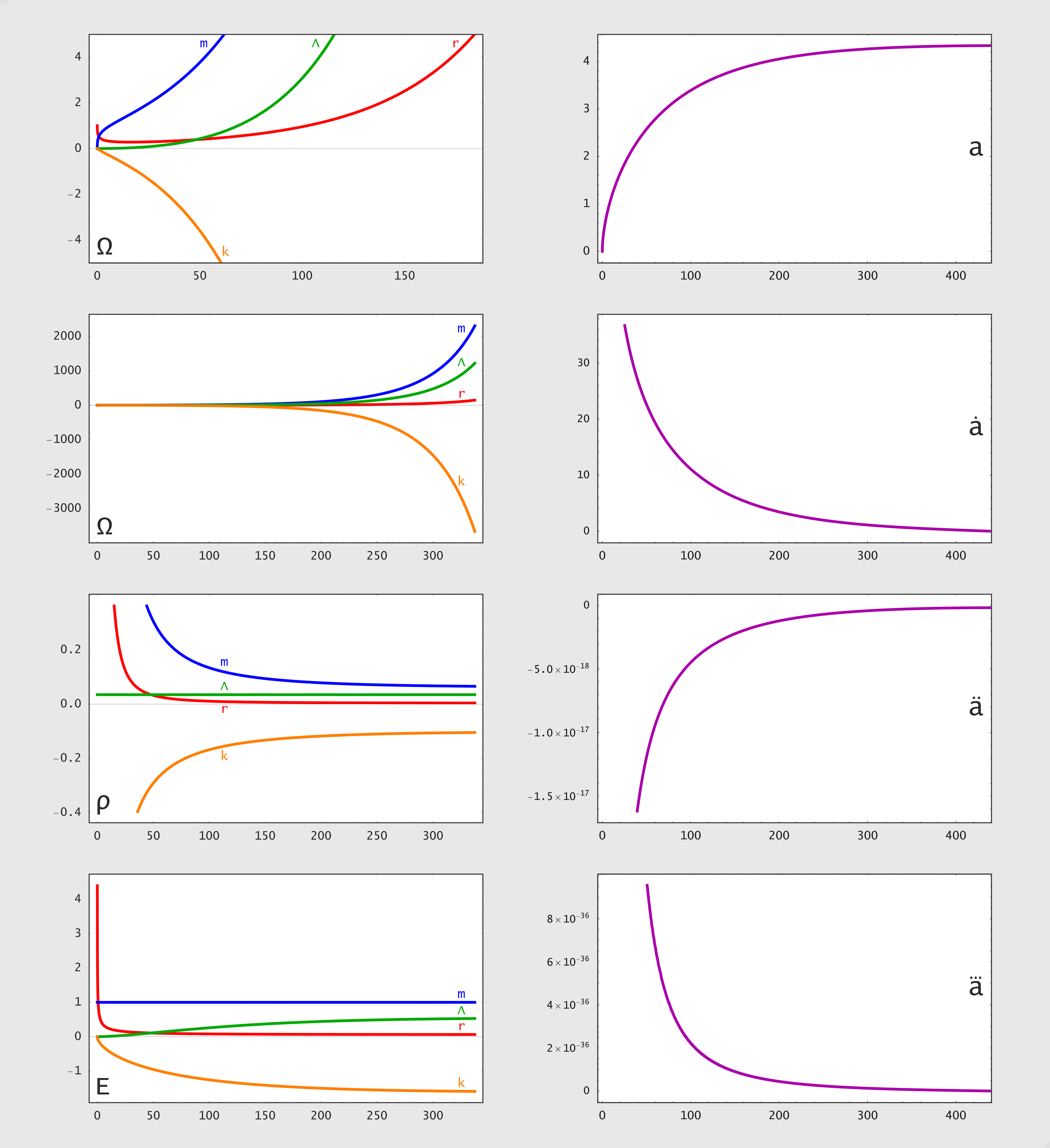
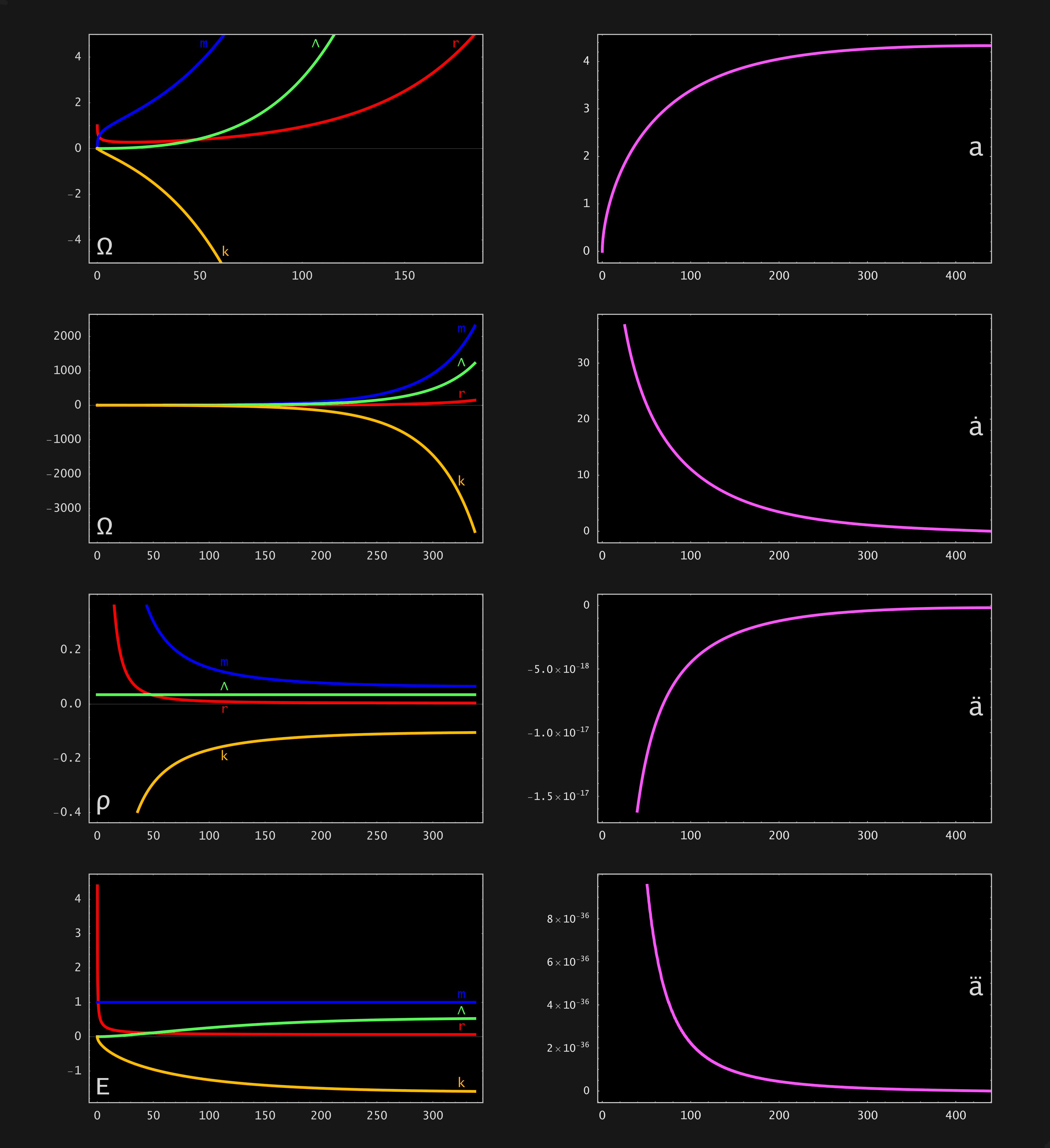
![]() Startparameters: H0=67.15, Ωr=0.3, Ωm=1.1, ΩΛ=0.0073226, Ωk=1-Ωr-Ωm-ΩΛ
Startparameters: H0=67.15, Ωr=0.3, Ωm=1.1, ΩΛ=0.0073226, Ωk=1-Ωr-Ωm-ΩΛ
![]() At a=4.334, t=440.1 the expansion stops (unstable state where ȧ=ä=â=0)
At a=4.334, t=440.1 the expansion stops (unstable state where ȧ=ä=â=0)
![]() Antipode: rM=πrK, Round trip: 2rM, Volume: V=2π²rK³, rK=c/H0/√[-Ωk/a²]
Antipode: rM=πrK, Round trip: 2rM, Volume: V=2π²rK³, rK=c/H0/√[-Ωk/a²]
![]() Colors: Worldlines, Hubbleradius, Antipode, Particlehorizon, Lightcone
Colors: Worldlines, Hubbleradius, Antipode, Particlehorizon, Lightcone
![]() Static | Crunch | Rip | Q | Light | Matter | Milne | Hyper | Λk | ΛCDM
Static | Crunch | Rip | Q | Light | Matter | Milne | Hyper | Λk | ΛCDM
![proper distance by cosmic time r(t). Y: t [0..80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.proper.1.png)
![proper distance by cosmic time r(t). Y: t [0..80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.proper.1.i.png)
![comoving distance by cosmic time R(t). Y: t [0..80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.comoving.1.png)
![comoving distance by cosmic time R(t). Y: t [0..80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.comoving.1.i.png)
![comoving distance by conformal time R(η). Y: η=RP/c [0...80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.conformal.1.png)
![comoving distance by conformal time R(η). Y: η=RP/c [0...80 Gyr], X: R [0..±80 Glyr], lightcone origin at a=1, t=8.10299 Gyr](closed.static.conformal.1.i.png)
![proper distance by cosmic time r(t). Y: t [0..800 Gyr], X: R [0..±800 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-proper.png)
![proper distance by cosmic time r(t). Y: t [0..800 Gyr], X: R [0..±800 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-proper-i.png)
![comoving distance by cosmic time R(t). Y: t [0..800 Gyr], X: R [0..±184.584 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-comoving.png)
![comoving distance by cosmic time R(t). Y: t [0..800 Gyr], X: R [0..±184.584 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-comoving-i.png)
![comoving distance by conformal time R(η). Y: η=RP/c [0...184.584 Gyr], X: R [0..±184.584 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-conformal.png)
![comoving distance by conformal time R(η). Y: η=RP/c [0...184.584 Gyr], X: R [0..±184.584 Glyr], lightcone origin at a=4.334, t=440.1 Gyr](closed-static-conformal-i.png)
![polar projection of R(t), R(a) & R(η) onto φ(Я). Я: t [0..440.1 Gyr] (left), Я: a [0..4.334] (middle), Я: η [0..140.737 Gyr] (right), φ: R [0..±71.6772 Glyr] (all), backward lightcone origin at the moment when the universe becomes static](closed.static.polar.png)
![polar projection of R(t), R(a) & R(η) onto φ(Я). Я: t [0..440.1 Gyr] (left), Я: a [0..4.334] (middle), Я: η [0..140.737 Gyr] (right), φ: R [0..±71.6772 Glyr] (all), backward lightcone origin at the moment when the universe becomes static. the particle horizon and past light cone extend over the antipode where they reenter from the opposite side](closed.static.polar.i.png)
![]() Static | Crunch | Rip | Q | Light | Matter | Milne | Hyper | Λk | ΛCDM
Static | Crunch | Rip | Q | Light | Matter | Milne | Hyper | Λk | ΛCDM
![]()
![]()
![]() Main
Main ![]() |
| ![]() Code | Info | a, ȧ, ä, ã, â, H, Ḣ, Ḧ, rH, rE, rP, rL, Σr, Ω
Code | Info | a, ȧ, ä, ã, â, H, Ḣ, Ḧ, rH, rE, rP, rL, Σr, Ω